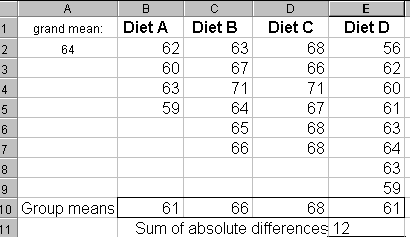
We can test by combining all the coagulation times in a hat, shuffling them, and dealing them out in groups of 4, 6, 6 and 8. Then we recalculate the sum of absolute differences among group means and observe whether it is ≥ 12.
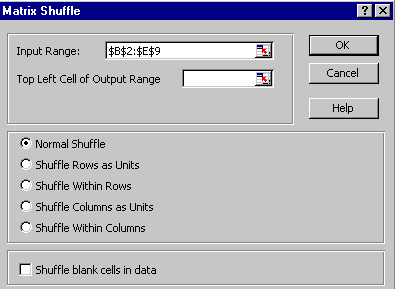
Select the data to be shuffled or resampled (here b2:e9):
Because we have selected a matrix, we are prompted to specify whether we want a normal (fully combined) shuffle, a shuffle of rows/columns taken as units, or a within-rows/columns shuffle.
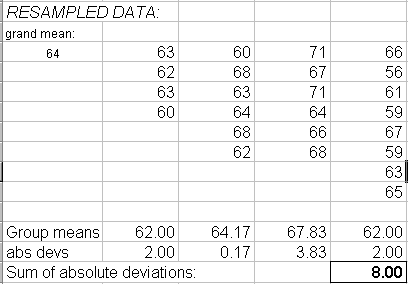
Leaving the “normal shuffle” box checked, we get output which observes the same row/column structure, but in which all the values have been shuffled and redistributed across all columns and rows:
In this shuffle, the randomly shuffled coagulation times (group means differing by a sum of 8) did not differ as much as in the real experiment (group means differing by a sum of 12). One shuffling does not signify, so we want to repeat the procedure many times, each time keeping score of the statistic of interest (the sum of absolute deviations among the group means).

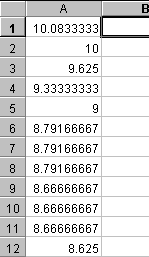
The final result will be an output sheet with the 10,000 shuffled values of the highlighted cell (each one the product of a different shuffling of the data):
In this case, you can see that the resampled value of the test statistic (sum of absolute deviations) was never as great as the observed value of 12, so we conclude that the sample means differ from one another to a greater extent than might arise by chance.